Dive Theory
The Physics of Diving
12 New PADI Instructor Exams (with the all important answers)
Now Available to Purchase from IDC Guide
If you want to receive IDC and IE Revision Documents as well as the very important PADI Mock IDC exams via email directly to your inbox you can receive 12 Complete PADI IDC mock exams (Dive Standards and Dive Theory) along with 25 Revision Documents. You can purchase them and other revision documents from this page IDC Guide Exam Revision Packs
There is plenty of Physics Revision below and also more Physics Revision Basics
-
Quick View -
Quick View
-
Quick View
-
Quick View
Water & Heat
Water removes body heat quicker than air
- It is 20 times a better conductor than air
- Water is 770 times more dense than air
- 3200 times more heat is required to raise to same temperature water, than air of the same volume
Heat Transmission
- Conduction (heat removal via direct contact)
- Convection (heat removal via fluids)
- Radiation (heat removal via electromagnetic waves) Divers are mostly affected by Conduction – water is a very good conductor
Water & Light
Visible light penetration in clear water:-
| Starts to go at | Gone by | |
| RED | 1m | 5m |
| ORANGE | 5m | 16m |
| YELLOW | 22m | 30m |
| GREEN | 50m | 76m |
| VIOLET | 4.5m | 30m |
Only 20% of sunlight reaches 10m in clear water, Colours are absorbed by depth
Fluorescents retain colour underwater because their wavelengths are not common and they emit colour when stimulated by light of any shorter wavelength.
Light – Made up of electromagnetic energy Water affects light through: The speed of light depends on the density of the medium it’s traveling through. The denser the medium, the slower the speed.
- Diffusion
- Absorption
- Refraction
- Turbidity
Diffusion: Scattering of light (prevents light reaching a certain depth)
Absorption: Absorbs the weakest wavelengths first i.e. red, orange, yellow, violet.. As less light is available the eye’s pupil opens up, resulting in less colour detail.
Fluorescents can be seen underwater, why?
They Don’t simply reflect colour. They emit colour when stimulated by light of any shorter wavelength
Refraction: Apparent size & closeness is affected by refraction
Light bends as it passes from air to water, due to water being more dense, therefore light slows in speed
Divers – Objects appear closer by ratio of 4:3 (an object 4 meters, will appear 3 meters away)
Size Refraction causes the size of an object to be magnified – approx.33%
Turbidity: The concentration of suspended particles – i.e. silt, rainwater runoff In highly Turbid water, objects at a distance appear further away than they appear (VISUAL REVERSAL).Turbidity is the most important factor affecting VISUAL REVERSAL
Reflection Affects light i.e. the light from the sun does no reflect from the surface of the water when the sun is directly above
Water & Sound
Sound travels in waves with acoustical energy (a form of mechanical energy).
Light can exist apart from matter, sound exists only within matter (cannot travel in vacuum i.e. space).
Speed: Sound travels best in dense matter i.e. travels better in water (solids or liquids) than air (gas). Therefore as water temperature changes, so does the affect of sound travel.
At 15 degrees Celsius, water transmits sound at 1410 meters per second (fresh), 1550 (salt) – 4 times faster than air Sound travels faster in water due to elasticity, not density (but denser matter =more elasticity)
RESULT: Divers can hear better and at more distance than on air
Direction: Direction difficult for diver, due to the high speed that sound travels – eardrums cannot work out (seems like sound from overhead)
SUMMARY
Water conducts heat (from our body 20 times) more efficiently than air by
CONDUCTION (Radiation = least effect)
The bending of light is called REFRACTION. Water absorbs colour – RED disappears first.
Sound travels 4 times faster in water (is denser / thicker than air) and always sounds as if it is coming from above you
Object appear to be 33% larger and 25% closer underwater (ratio 4:3) due to REFRACTION
VISUAL REVERSAL is when objects appear to be further away than they really are (due to turbidity)
Daltons Law
Pressure (density) & Partial pressure of gases Oxygen Helium Nitrogen Carbon Dioxide
The sum of gases will always equal a whole (100%)
As the pressure increases (gets more), the partial pressure (NOT THE PERCENTAGE, THE PERCENTAGE NEVER CHANGES) will increase (get more)
Daltons Law
Pressure (density) & Partial pressure of gases Oxygen Helium Nitrogen Carbon Dioxide
The sum of gases will always equal a whole (100%)
As the pressure increases (gets more), the partial pressure (NOT THE PERCENTAGE, THE PERCENTAGE NEVER CHANGES) will increase (get more)
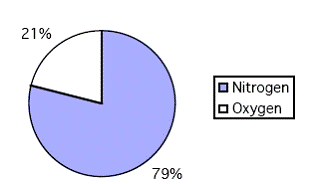
Approximations made 21% Oxygen + 79% Nitrogen = 100% Air
The atmosphere really consists of:
| Nitrogen | = | 78.084% |
| Oxygen | = | 20.946% |
| Argon | = | 0.934% |
| Carbon Dioxide | = | 0.033% |
Neon, Krypton, Hydrogen, Xenon Radon, and Carbon Monoxide = 0.003%
Consider it as 79% nitrogen and 21% oxygen (SSI use 80% and 20%)
Nitrogen = N2
Oxygen = O2
0.21 oxygen (Bar)
| 0.79 nitrogen (Bar) + |
| 1.0 BAR / 1 ATM (sea level) |
100% air will always be 100% no matter what gas mix is used
10m = 2 BAR (2 BAR x 0.21) = 0.42 oxygen (BAR)
| + (2 BAR x 0.79) = 1.58 nitrogen (BAR) |
2 BAR |
30m = 4 BAR (4 BAR x 0.21) = 0.84 oxygen (BAR)
| + (4 BAR x 0.79) = 3.16 nitrogen (BAR) |
4 BAR |
This can be used with any gas mix such as Helium, Nitrogen,Carbon Dioxide, etc.
E.g. Nitrox 36% at 20m (3 Bar)
= 0.36 x 3 (Bar)
= 1.08 Bar
Diving
Air =21% Oxygen 79% Nitrogen (ALWAYS) This is important to be able to calculate the partial pressure of gases to any depth. Doing this you’ll be able to see when Oxygen reaches high levels that may cause oxygen toxicity.
1.4 Bar (Maximum)
1.6 Bar (Contingency)
Therefore is an air mix has 0.2% carbon monoxide. Breathing it at 30m would be the equivalent of breathing what percent at the surface?
30m = 4ata; 4 x 0.2% = 0.8%
Henrys Law
Gases & Liquids
If the pressure increases (gets more), the more gas will be dissolved (go into) the liquid. If the pressure is decreased (gets less), the gas will come out of the liquid
E.g. If you shake a Coca-Cola bottle, you’re building up pressure inside the bottle, forcing gas into the cola. When you quickly open the bottle you decrease the pressure and all the gas comes out of the cola. THE BUBBLES!
Saturation:
When the pressure (an amount) of gas that has been forced into a liquid is the same as the surrounding pressure (outside pressure). Like when shaking the Coca-cola bottle, you can shake it all you want until there is no more gas to be dissolved. It has reached an equal pressure so the pressure is therefore the same inside the bottle as the pressure outside the bottle.
Super-saturation:
When the pressure becomes less, the same as when you open the Coca-Cola bottle, the gas that was dissolved into the liquid starts coming out of the liquid (out of solution). If it is controlled the bubbles come out slowly. However, if the pressure is released too fast, the bubbles will come out too fast as well.
Charles Law
Temperature & Pressure (density)
The amount of change in either volume or pressure of a given volume, is proportional to temperature changes
As the temperature increases (gets more) the volume of a flexible container will increase (get more) and the density (pressure) inside the container (non-flexible) will increase and if the container is flexible the density (pressure) will remain constant.
The opposite happens when the temperature decreases (gets less). As the temperature decreases (gets less) the volume of a flexible container will decrease (get less) and the density (pressure) inside the container (non-flexible) will decrease (get less) the flexible containers density (pressure) will remain constant.
FOR EVERY 1 DEGREE CELCIUS CHANGE (up or down) IN TEMPERATURE THERE IS A 0.6 BAR CHANGE IN PRESSURE
Example if a tank is 200 Bar and on the boat in the sun at 40 Degrees Celsius, what pressure would the tank be if someone puts the tank on and jumps in the water which is 20 Degrees Celsius ?
Answer 200 – ( 20 * .6) = 188 Bar
More heat = more volume / more density
Air molecules move fast because its so hot causing more density (pressure)
Less heat = less volume / less density
Air molecules stay closer together causing less density (pressure)
Further revision
This level of understanding is normally not required but if you can understand this all the better, in general just remember .6 degrees for every 1 bar as in the above example.
If a gas temperature rises and the volume stays constant, pressure increases. If temperature rises and the pressure stays constant, volume increases.
General rule:-
For every 1 deg C, change a scuba tank changes 0.6 bar.
Charles Law combined with Boyle’s Law:-
P1 V1 / T1 = P2 V2 / T2
Given the problem:
A gas occupies a volume of 20 L at a pressure of 5 atm and a temperature of 500K. What will the volume be if both the pressure is raised to 10 atm and temperature is changed to 250K?
Let’s rewrite to put in the variables:
A gas occupies a volume of 20 L (V1) at a pressure of 5 atm (P1) and a temperature of 500K (T1). What will the volume (V2) be if both the pressure is raised to 10 atm (P2) and temperature is changed to 250K (T2)?
Substituting into the equation
P1 V1 / T1 = P2 V2 / T2
we get:
(5 atm ) (20 litre) / 500K = (10 atm) ( V2) / 250K
Solving for V2,
(5 atm) (20 L) (250 K) / ( 10 atm) (500 K) = V2 = 5 L.
Now let’s see if you can do one:
A gas occupies a volume of 200 litres at a pressure of 2 atm and a temperature of 300 K. What will be the volume if both the pressure is raised to 10 atm and the temperature is changed to 1000 K?
(Note:- The exact answer is approx. 0.6% less).
A 12 litre tank reaches 52 C while filling to 200 bar. The tank goes into water at 7 C. What will the tank pressure be?
General Rule Calculation:-
52 – 7 = 45 x 0.6 = 27
200 – 27 = 173 bar
or
P1 P2 200 + 1 P2 201 P2
___ = ___ _______ = _______ ___ = ____
T1 T2 52 + 273 7 + 273 325 280
280 x 201 / 325 = P2
56280 / 325 = 173.1 – 1 = 172.1 bar
Ok but will this ever affect me ?
In the real world the main time this will affect you is when you are on a sunny boat at lunchtime after your morning dive and you get your tanks filled, your students check them as part of their pre-dive checks (Remember BWRAF) and then complain that they have 10 bar left after jumping in to cold water and waiting around before descending. I always do a quick air check after the descent just to keep myself aware of this, you will be amazed how much air some people use at the start of their dives trying to descent
Boyles Law
This law affects you every dive, it’s the reason why you need to clear you ears, why your wetsuit gets compressed as you descent, the reason why your bubbles get bigger as they race to the surface and the reason why the deeper you go the more air you use and the less bottom time you have, so you really need to know about it J
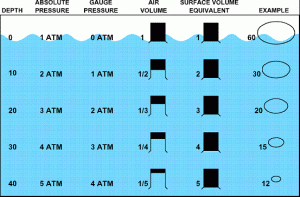
in the diagram below you can seee that as depth increases the pressure (which is measured in bar increases. Therefore a diver at 30m, which is the depth a qualified open water dive can descent to, will be under 4 bar of pressure. The 4 bar comes from 1 bar from the weight of the atmosphere and the 3bar from the weight of the water above him.
Due to the increase in pressure the volume of air reduces , it is worth poining out that the volume of air in your tank does not change as you descent but when you exhale from your regulator at depth that air is then exposed to pressure and as teh air travels to the surface it will be exposed to less and less pressure so will your bubbles increase in size all the way to the surface
Boyle’s law deals with the relationship between pressure and volume.
For the purposes of explanation and calculations we assume no changes in temperature.
This states that for a fixed quantity of gas (at constant temperature) the volume of the gas is inversely proportional to the pressure of the gas. If you take a bucket with an internal volume of 1 litre and turn it upside down in the water, then take it down to a depth of 10 metres, because the ambient pressure at 10 metres depth is twice the pressure of the surface, the volume of air in the bucket reduces in volume by half to 1/2 a litre.
Alternatively if you start at 10 metres depth and half fill the bucket with air, then ascend to the surface, the ambient pressure will be halved, so the volume inside the bucket will double, and fill up completely.
Question: If the diagram was extended to 60m what would the air volume and pressure be?
As the pressure surrounding an object increases (gets more) the volume will decrease (get less) and the density will increase (get more)
Gauge pressure = Water pressure (excluding atmospheric pressure)
20msw (metres of sea water) = 2 Bar
Ambient / Absolute pressure = Water pressure AND Atmospheric pressure
20msw (metres of sea water) = 2 Bar + 1 Bar Atmospheric pressure = 3 Bar
Example 1
A flexible container with a volume of 35 Litres is at 28mfw (metres of fresh water), and is taken to the surface. What will the new volume of the container be?
28mfw = 2.7 Bar (28 / 10.3) Gauge pressure + 1 Bar for Ambient pressure = 3.7 Bar
Volume of the container = 35 litres 35 (Litres) x 3.7 (Bar) = 129.5 Litres at the surface
If you were to take the same container back down to 24msw (metres of sea water) what would the new volume be? 28msw = 2.4 Bar (24 / 10) Gauge pressure
1 Bar for Ambient pressure = 3.4 Bar Volume of the container at the surface is 129.5 Litres – 129.5 (Litres) / 3.4 (Bar) = 38 Litres at 24m
Example 2
You take a gas volume of 27 litre from 32 m to 17 m in fresh water. What will the new volume be?
For Fresh Water:-
Correct for pressure change in fresh water (adding the 1 to account for surface atmospheric pressure)
32 / 10.3 = 3.10 + 1 = 4.10
17 / 10.3 = 1.65 + 1 = 2.65
So 27 litre x 4.10 = 110.7 at surface.
110.7 / 2.65 = 41.77 rounded = 41.8 litre at 17 m
For Salt Water:-
No pressure change requires because it is salt water.
3.2 + 1 = 4.2
1.7 + 1 = 2.7
So 27 x 4.2 = 113.4 / 2.7 = 42.0 litres at 17 m.
FACTS
10m SEA WATER = 1 BAR
E.g. 34m = 3.4 Bar gauge pressure
(34m / 10 = 3.4) + 1 Bar for Ambient pressure = 4.4 Bar
10.3m FRESH WATER = 1 BAR
E.g. 34m = 3.3 Bar gauge pressure
(34m / 10.3 = 3.3) + 1 Bar for Ambient pressure = 4.3 Bar
If you take a container filled with air up from a certain depth – the volume will increase (get bigger) and the air will become less dense (less pressure) You multiply (x) the volume when taking down. You divide (/) the volume when taking up If you have 2 different depths underwater. First calculate the volume at the surface, and then back down at new depth again.
Archimedes Principle
The Greek mathematician Archimedes determined that ‘An object wholly or partially immersed in a fluid is buoyed up by a force equal to the weight of the fluid displaced by the object’
An object that weighs less than the water it displaces will float and is POSITIVELY BUOYANT. It’s buoyancy is expressed as a positive number, such as being 2 kgs positive. An object that weighs exactly the same as the water it displaces with neither sink nor float and is NEUTRALLY BUOYANT. Adding or removing weight will make it sink or float. An object that weighs more than the water it displaces will sink and is NEGATIVELY BUOYANT. It’s buoyancy is expressed as a negative number, such as being 2 kgs negative To determine the buoyancy of an object in water you need to know:
The objects weight
How much water the object displaces (the objects volume)
The weight of the water displaced
THE DEPTH OF EITHER SALT WATER / FRESH WATER HAS NO EFFECT TO DETERMINE THE BUOYANCY OF THE OBJECT
OPEN WATER DIVER
O / W – D
Objects weight Sea = 1.03 OR Displacement
Fresh = 1.00
= ?
Example: You plan to recover a 150kg outboard motor in sea water that displaces 60 litres and lies at 30m. How much air must you put in a lifting device to make the motor neutrally buoyant?
Open (O) Objects weight = 150kg
Water (W) Water = 1.03kg (Sea)
Diver (D) Displacement = 60 litres
DEPTH = MEANS NOTHING!!!
(O) 150 / (divide by) (W) 1.03 – (subtract) (D) 60 = 85.6 Litres (of air)
FACTS
1 Litre of Salt Water = 1.03 KGS
1 Litre of Fresh Water = 1.00 KGS
If an object has either neutral or positive buoyancy in sea water and you take it into fresh water, the buoyancy cannot be determined without additional information HOWEVER If you take an object from fresh water to sea water you can determine the buoyancy of the object E.g. If an object is neutrally buoyant in fresh water it will be positively buoyant in sea water
Example:
You must sink into fresh water an object that weighs 50kg and displaces 300 litres. How much lead weight must you affix to the object to make it 10kg negative on the bottom?
Open (O) Objects weight = 50kg
Water (W) Water = 1.00kg (Fresh)
Diver (D) Displacement = 300 litres
(O) 50 / (divide by) (W) 1.00 – (subtract) (D) 300
= -250kg (positively buoyant) The object is 250kg positively buoyant. To make it 10kg
negative, first make it neutrally buoyant, and then 10kg
negatively buoyant
+ (add) 250kg (to make neutral)
+ (add) 10kg more (to make it negative)
= 260kg (of lead weight)
AIR CONSUMPTION
Air becomes denser (more pressure) as you descend underwater. A diver will use more air due to increased (more) pressure. He’s going deeper…more pressure. A diver will use less air due to the decreased (less) pressure as he ascends. He’s going up… less pressure.
E.g. A divers air consumption rate is 3 Bar per minute at the surface. What will the air density be at 30m compared to the surface, and what will the divers air consumption be?
4 times as dense (30m = 4 Bar)
12 Bar per minute (3 Bar x 4 Bar)
Pressure increases by 1.0 Bar in 10m of Salt Water
18m = 1.8 Bar gauge pressure (18m / 10 = 1.8)
+ 1 Bar for Ambient pressure = 2.8 Bar
Pressure increases by 1.0 Bar in 10.3m Fresh Water
18m = 1.75 Bar gauge (18m / 10.3= 1.75)
+1 Bar for Ambient pressure = 2.75 Bar
You multiply (x) the volume of the air the diver uses when the diver descends (goes down deeper) You divide (/) the volume of the air the diver uses when the diver ascends (comes up shallower)
More Dive theory that I will get categorised shortly.
PADI Mock Exams
Please check and review your revision progress so far using these PADI Mock IDC Exams.
PADI Dive Theory Exam C as well as PADI Dive Standards Exam C
Buy the complete IDC revision packs that now include lots more (another 8) practice mock exams, the exams include all the questions and answers you will need to revise to PASS the PADI IDC.
If you found this page helpful, please see the Mega Revision Pack. It contains over 12 mock exams to practise with as well as a large variety of IDC/IE revision resources.